Dmitry A. Garanin - Research
General direction of my research is Theory
of Magnetic Phenomena and Statistical Physics, including
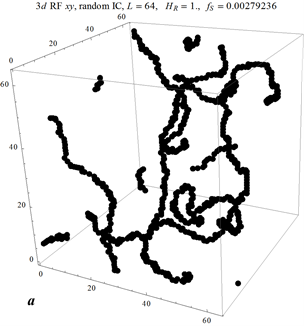
Theoretical arguments of 70th by Imry & Ma, Larkin, and Chudnovsky predict that whatever small random field or random anisotropy would destroy a long-range order in magnetic and other system (vortex lattice in superconductors, charge-density waves, etc.). Using modern computer power and advanced numerical algorithms, we are carrying out an extensive investigation of ordering in different models described by n-component classical spins in d dimensions. Contrary to theoretical expectations, we have found that initially ordered systems only partially disorder if the system supports singularities (vortices and vortex lines, hedgehogs) or smooth topological structures (kinks, skyrmions). The former exist for n ≤ d, and necessarily arize in the completely disordered Imry-Ma state, as follows from our new topological argument. As creating singularities cost energy, the Imry-Ma state is not the ground state of the system and the system remains partially ordered. The case n = d + 1 is a marginal case. Although the IM state is the grounds state, the system cannot reach it by relaxation because of conservation of the topological charge (e.g., of skyrmions). We have published a big paper on the 3D random-field xy model (n = 2) [Phys. Rev. B 88, 224418 (2013)] and a Letter [Phys. Rev. Lett. 112, 097201 (2014)] containing the above general arguments illustrated by numerical results. In the large follow-up paper [Eur. Phys. J. B 88, 81 (2015) ] we numerically investigated the random-field model for any d and n in depth and found that the only model whose ground state is not fully disordered is 3D xy model.
Pinned vortex lines in the 3d random-field xy model I am especially interested in the so-called "PhononBottleneck" problem in the spin-lattice relaxation that has not recieved a proper analytical treatment since 1941. While first steps have been done in Spring 2006 and two papers have been published [Phys. Rev. B 75, 094409 (2007) and Phys. Rev. B 77, 024429 (2008)], a lot of new efforts are due, both on the way of analytics and numerical calculations for quantum and classical models. A possible competition between the phonon bottleneck (that tends to suppress spin relaxation) and the photon [Phys. Rev. Lett. 89, 157201 (2002)] and phonon [Phys. Rev. Lett. 93, 257205 (2004)] superradiance (that tends to increase spin relaxation) is an exciting question to be investigated.
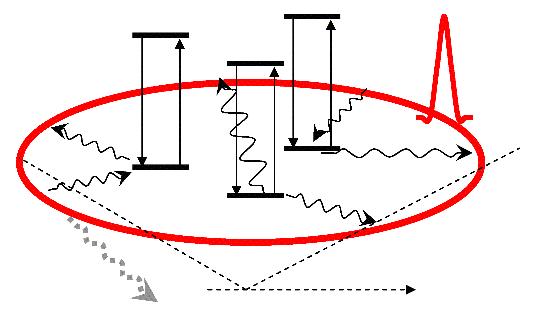
The phonon bottleneck: Emitted phonons are being reabsorbed by spins and thus spin-lattice relaxation slows down dramatically Right now the so-called Landau-Lifshitz-Bloch (LLB) equation of motion for the magnetization at finite temperatures, derived in 90th [see, e.g., Phys. Rev. B 55, 3050–3057 (1997)], becomes the best candidate to be applied to the processes of thermal magnetic recording. The LLB equation describes both transverse and longitudinal relaxation of the magnetization vector. My colleagues and I are further developing the aspects of the LLB equation that are important for industrial applications in magnetic information storage.
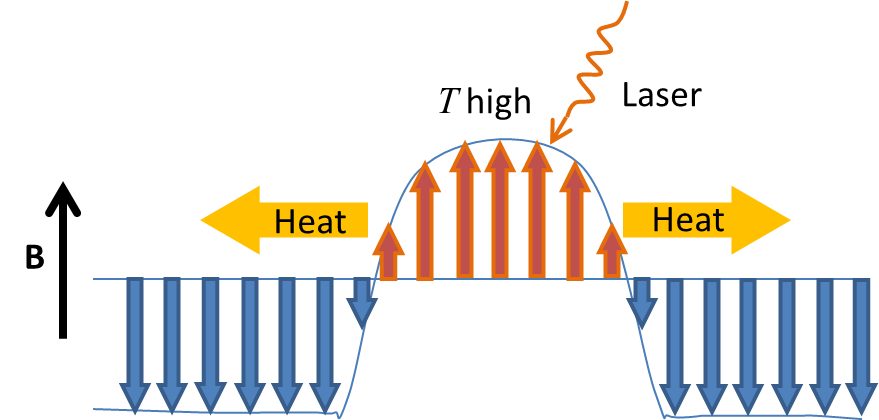
LLB equation captures dynamics of the magnetization length and can be used to describe the effect of heating in fast magnetization reversal We are continuing working on the beautiful parameter-free spin-phonon interaction that in the rotating lattice frame has the form as simple as -W·S [Phys. Rev. B 72, 094426 (2005)]. This very basic interaction that allows to obtain some new model-independent results in spin relaxation and rederive some old results in a simple way, has confused a number of theorists. Another hot topic is the magnetic burning or deflagration that recently was experimentally observed by Myriam Sarachik's group at the City College of the CUNY and by Javier Tejada's group at the University of Barcelona. Although the first and simplest theory of the magnetic burning has been recently published (Suzuki et al, PRL 2005) that were a lot of questions to be clarified such as the role of spin tunneling and the ignition of the magnetic avalanch. Here is the support page with animations and link to our first paper on magnetic deflagration, Phys. Rev. B 76, 054410-(13) (2007).
Magnetic deflagration (burning): Decay of a metastable state triggered by the temperature Continuing the research on magnetic deflagration, we discovered fronts of spin tunneling in molecular magnets [Phys. Rev. Lett. 102, 097206-(4) (2009), Phys. Rev. B 80, 014406-(11) (2009)]. This is the so-called "cold" or quantum deflagration. In contrast to the standard deflagration, here the parameter controlling the escape rate of magnetic molecules out of the metastable state is not temperature but the dipolar field produced by the magnetic molecules themselves. This self-consistent dipolar field can bring the system on or off tunneling resonance. We have shown that the system of magnetic molecules self-organizes in such a way that the molecules are on resonance in a broad region along the propagation direction, thus facilitating tunneling and motion of the front.
"Cold" or quantum magnetic deflagration: Decay of the metastable state via resonance quantum transition controlled by the dipolar field With PhD student Reem Jaafar and further with undergraduate student Saaber Shoyeb we incorporated both thermal and quantum effects in our generalized theory of magnetic deflagration in 1d, [Phys. Rev. B 81, 180401(R) (2010) and Phys. Rev. B 85, 094403 (2012)]. The full 3d theory of this process is presented in my paper Turbulent fronts of quantum detonation in molecular magnets [Phys. Rev. B 88, 064413 (2013) ]. This spectacular effect is still waiting for an experimental realization.
Quantum detonation fronts in Mn-12 One more of my areas of interest is magnetomechanical effects in nanomagnets related to conservation of the angular momentum. Recently E. M. Chudnovsky and I have shown that the problem of spin tunneling in a rigid nanoparticle has a beautiful analytical solution. If the particle's moment of inertia is below some critical value, the spin cannot tunnel and localizes in one of the up/down states. The EPL article of our PHD student Reem Jaafar considering a single magnetic molecule rotating between conducting leads has been chosen for a feature in Europhysics News and has been featured in Lehman Today. A new type of spin decoherence arises from interaction of an embedded spin with a torsional cantilever, Phys. Rev. X 1, 011005 (2011).
Spin tunneling transitions excite torsional cantilever During the last years we worked a lot on skyrmions that are topological formations in 2D Heisenberg magnets
Neel skyrmion Although within the continuous approxomation (field theory) skyrmions are stable and their energy does not depend of their size, we have found that skyrmions collapse in the pure-exchange 2d magnets because of the discreteness of the lattice. With our PhD student Liufei Cai we have calculated analytically and numerically the lifetime of skyrmions in both ferro- and antiferromagnets in Phys. Rev. B 86, 024429 (2012). Other interactions, such as dipole-dipole interaction and Dzialoshinskii-Moriya interaction (DMI) can stabilize skyrmions.
1) Skyrmion and a gas of emitted spin waves; 2) Spin waves carry away the
remaining energy of a collapsed skyrmion. Vertical axis: Mz. In systems with DMI, skyrmions repel each other via the interaction energy exponential in the distance, as found numerically in our work with our PhD student Daniel Capic [J. Phys.: Condens. Matter 32, 415803 (2020)]. This allows considering skyrmions in some cases as point particles with repulsion.
Pair of skyrmions has a positive repulsion energy because of the deformation of the spin field in the region between the skyrmions. Recently we investigated the melting of the skyrmion lattice by considering skyrmions as point particles with repulsion [Phys. Rev. B 107, 014419 (2023)]. In the ordered phase, skyrmions arrange themselves in a hexagonal lattice. The equilibrium number of skyrmions in the system can be found by minimizing the total energy being the negative self-energy of each skyrmion plus the positive energy of their repulsion that we have found in 2020. With increasing the temperature, skyrmion lattice melts and becomes a skyrmion liquid. Skyrmion lattice can also be a polycrystal, in particular, under the influence of rigid walls that favor the orientation of hexagons parallel to the boundary (see picture below).
Polycrystalline skyrmion lattice bound by a circular rigid wall. Orientation of hexagons is color coded. These are my main current external collaborations:
Faculty Recognition Award for Research - 2010 - My prepared speech |